菲涅尔计算式以及近似公式

比较有名的Schink近似式。本身的计算式并不难，就是描述光在两个介质中反射光强度和折射光强度的规律。

菲涅尔方程（Fresnel equations），也称为菲涅尔条件，是描述光在两种不同介质界面处反射和折射行为的一组公式。这些方程由法国物理学家奥古斯丁·让·菲涅耳于19世纪初提出，主要用于计算入射光、反射光和折射光之间的振幅比。根据光的偏振状态，菲涅尔方程分为两种情况：平行偏振光（s偏振或TE模式）和垂直偏振光（p偏振或TM模式）。

菲涅尔方程的基本形式

#

对于从介质1（折射率为(n_1)）以角度(\theta_1)入射到介质2（折射率为(n_2)）的平面波，其反射率(R)和透射率(T)可以通过以下方程计算：

对于s偏振光：

#

对于p偏振光：

#

其中，

反射率(R)可以由反射系数的模平方给出，即R=|r|²

什么是P光、什么是S光？

#

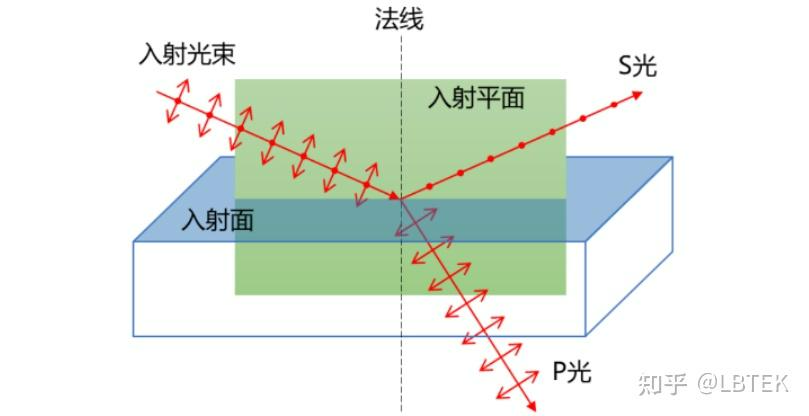
P光和S光是针对光的入射反射和折射来说的，此时，将入射光与反射光/折射光所在的平面定义为参考面，S光和P光分别为偏振方向垂直以及平行于该参考面的线偏振光。

举例而言，如下图所示，一束光照射到入射面上，形成反射和折射，将入射光束与法线所形成的平面定义为入射平面。P光（德文Parallel的首字母，意为平行的）是偏振方向与入射平面平行的光，而S光（德文Senkrecht的首字母，意为竖直的）是偏振方向与入射平面垂直的光。

Schlink近似

#

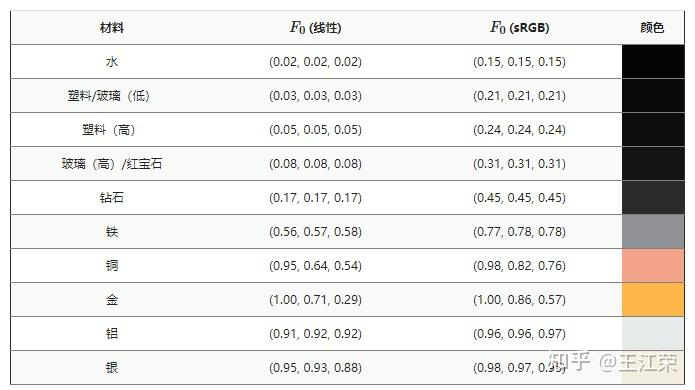
但是在图形学中，一般不会使用这种p光和s光的表达式，用于估算光在介质界面发生反射时的反射系数的一种简化公式，特别适用于计算机图形学中的光线追踪算法。

对于s偏振光和p偏振光，Schlick近似可以将p光和s光的反射率统一表达为：

用代码可以表示为：

vec3 fresnelSchlick(float cosTheta, vec3 R0)
{
    return R0 + (1.0 - R0) * pow(1.0 - cosTheta, 5.0);
}

其中：

• 

  是在给定入射角θ下的反射率。

• 

  是当光垂直入射（即θ=0）时的反射率，可以通过两种介质的折射率n1和n2计算得出：

  

• cos⁡θ是入射角的余弦值。

利用这个特点可以制作外发光。

引用：https://zhuanlan.zhihu.com/p/375746359