当fbx模型导入到Houdini的时候,会产生最基本的四个Class(或者说来自于fbx本身就是这四个Class):
- Points
- Primitives
- Vertices
- Polygons
我们在这里就拿RubberToy举例。
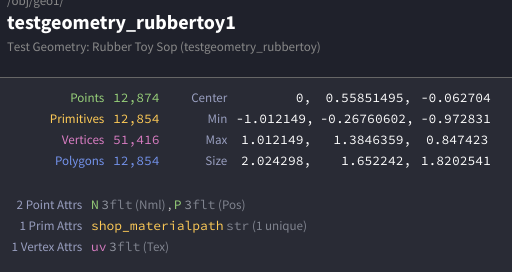
基本几何组件 #
Points(点) 是最基础的几何元素,每个点在3D空间中有一个位置坐标(x,y,z)。点可以独立存在,也可以作为其他几何元素的组成部分。
Vertices(顶点) 是连接点和图元的桥梁。一个顶点引用一个特定的点,但同一个点可以被多个顶点引用。顶点主要用于定义图元中点的顺序和连接关系。
Primitives(图元) 是由顶点组成的几何形状,比如多边形、曲线、体积等。每个图元包含一系列顶点,这些顶点定义了图元的形状和拓扑结构。
对于Polygons(多边形),一般情况下我们可以就认为是Primitives(即面)。在最后我再讨论一下Polygons和Primitives的不同之处。
属性系统 #
Houdini使用强大的属性系统来存储数据。属性可以附加到不同的几何组件上:
Point属性 存储在点上,比如位置(P)、颜色(Cd)、法线(N)等。这些属性会在点之间进行插值。
Vertex属性 存储在顶点上,常用于UV坐标、顶点颜色等需要在同一个点的不同面上有不同值的情况。
Primitive属性 存储在图元上,比如材质ID、面的类型等。整个图元共享同一个属性值。
Detail属性 是全局属性,存储在整个几何体上,比如总的点数量、时间信息等。
我用一个简单的例子来解释这三者的区别:
想象一个立方体 #
Points(点) 就像是立方体的8个角。每个角在空间中有一个固定的坐标位置,比如(0,0,0)、(1,0,0)等等。
Primitives(图元) 就是立方体的6个面。每个面都是一个四边形,需要4个点来定义。比如底面可能由点1、2、3、4组成。
Vertices(顶点) 是连接点和面的"引用"。因为同一个点(比如立方体的一个角)会被3个不同的面共享,所以需要3个不同的顶点来分别引用这个点。
关键区别 #
想象立方体的一个角点,这个角点的坐标是固定的(比如原点),但是:
- 这个点只有一个位置坐标
- 但有3个顶点分别属于3个不同的面,都指向这同一个点
- 这样每个面(图元)就可以给自己的顶点设置不同的属性
为什么需要这样设计? #
比如你想给立方体贴纹理,同一个角点在不同面上的UV坐标是不同的:
- 在正面,这个点的UV可能是(0,0)
- 在右面,这个点的UV可能是(1,0)
- 在顶面,这个点的UV可能是(0,1)
如果没有顶点这个中间层,就无法实现同一个点在不同面上有不同的属性值。
简单说:点定义位置,图元(Primitives)定义形状,顶点让同一个点在不同图元中可以有不同属性。
这就引申到了对于Vertices的表示方式。还是拿我们之前的立方体。简单来说,我们可以这么理解:
一个Point连接着三个面
- 被第一个面的Vertices引用,序号为2
- 被第二个面的Vertices引用,序号为3
- 被第三个面的Vertices引用,序号为1
Vertices存在的最大意义就是可以对每一个面进行单独的控制(比如Temp,比如TTL,比如Gravity)。因为如果单独为Point赋值,那么每一个被链接的面都会被赋予同一个颜色。
Vertices的双重身份 #
Vertices有两个编号可选。分别是全局编号和复合标识。
全局编号:每个vertex有一个全局唯一的编号(@vtxnum),从0开始递增。
复合标识:vertex同时可以用<primnum>:<vertex_in_prim>的格式来标识,也就是”面编号+顶点编号“,表示"某个图元中的第几个顶点"。
对,这是正确的!在Houdini中,vertex确实有一个复合标识系统:
Vertex的双重标识 #
全局编号:每个vertex有一个全局唯一的编号(@vtxnum),从0开始递增。
复合标识:vertex同时可以用<primnum>:<vertex_in_prim>的格式来标识,表示"某个图元中的第几个顶点"。
假设有在一个一个四边形(quad):
- 这个四边形是0号图元(@primnum = 0)
- 它有4个顶点,在这个图元内的编号是0,1,2,3
- 所以这4个顶点可以表示为:0:0, 0:1, 0:2, 0:3
VEX #
// 获取图元中的顶点数量
primvertexcount(0, @primnum)
// 获取图元中第i个顶点的全局编号
primvertex(0, @primnum, i)
// 获取顶点在其所属图元中的局部编号
primvertexindex(0, @vtxnum)
实际应用 #
// 在primitive wrangle中遍历当前图元的所有顶点
int vtx_count = primvertexcount(0, @primnum);
for(int i = 0; i < vtx_count; i++) {
int vtx = primvertex(0, @primnum, i); // 获取第i个顶点的全局编号
// 现在可以操作这个顶点
setvertexattrib(0, "Cd", vtx, {1,0,0});//归零color
}
所以vertex既有全局的线性编号,也有基于图元的层次化标识,这让在不同上下文中引用顶点变得很灵活。
在VEX中有多种方式来操作和引用vertex,这里是主要的写法:
从图元获取顶点:
// 获取当前图元的第0个顶点
int vtx = primvertex(0, @primnum, 0);
// 获取图元的所有顶点
int vtx_count = primvertexcount(0, @primnum);
for(int i = 0; i < vtx_count; i++) {
int vtx = primvertex(0, @primnum, i);
}
从点获取顶点:
// 获取点的第一个顶点
int vtx = pointvertex(0, @ptnum);
// 获取点的所有顶点
int vtx_array[] = pointvertices(0, @ptnum);
获取和设置Vertex属性 #
读取vertex属性:
// 直接在vertex wrangle中
vector uv = @uv;
vector color = @Cd;
// 从其他地方读取特定vertex的属性
vector uv = vertex(0, "uv", vtx_num);
vector color = vertex(0, "Cd", vtx_num);
设置vertex属性:
// 在vertex wrangle中直接设置
@uv = {0.5, 0.5};
@Cd = {1, 0, 0};
// 从其他地方设置特定vertex的属性
setvertexattrib(0, "uv", vtx_num, {0.5, 0.5});
setvertexattrib(0, "Cd", vtx_num, {1, 0, 0});
Vertex与Point/Primitive的转换 #
// vertex到point
int pt = vertexpoint(0, @vtxnum);
// vertex到primitive
int prim = vertexprim(0, @vtxnum);
// vertex在primitive中的局部索引
int local_idx = primvertexindex(0, @vtxnum);
实际应用例子 #
为每个面的顶点设置不同UV:
// 在primitive wrangle中
int vtx_count = primvertexcount(0, @primnum);
for(int i = 0; i < vtx_count; i++) {
int vtx = primvertex(0, @primnum, i);
vector uv = {float(i)/vtx_count, 0.5};
setvertexattrib(0, "uv", vtx, uv);
}
创建硬边效果:
// 在vertex wrangle中,根据所属面设置颜色
int prim = vertexprim(0, @vtxnum);
@Cd = rand(prim); // 同一面的所有顶点颜色相同
这些方法让你能够在VEX中灵活地操作vertex属性,实现各种复杂的几何处理效果。
但是说实话,在一般情况下,Point和Vertex(Vertices)其实是差不多的东西。但Houdini会在颜色处理中处理这些比较微小的差异:
Point Cd:颜色在面之间平滑插值
- 适合:渐变效果、基于位置的着色
Vertex Cd:可以产生硬边界
- 适合:每个面不同材质、硬边光照、UV接缝处。
比如说我们如果创建一个立方体,给其中一个角点设置红色:
- 用Point Cd:这个角的红色会在3个相邻面间平滑混合。即颜色会在每个面之间做平滑的渐变。
- 用Vertex Cd:可以让这个角在3个面上显示完全不同的颜色
所以说,在简单模型上看起来差别不大,但vertex Cd的灵活性在于能打破point的颜色约束,实现更复杂的着色需求。大部分时候point Cd就够用了。
Houdini的Polygons和Primitives之间有什么不同? #
虽然说在日常的使用中,可以看到在大部分的情况下,Houdini就是将Primitives等价于Polygons;选择的时候,选中了面则会提醒你这是Primitives;比如说PolyExtrude,PolyBevel这种,直接将Primitive等价于Polygons。所以在一般的口头交流中,这几乎是等价的,并且通常不会产生歧义。
为什么不一定完全精确? #
从Houdini的底层几何结构来看,“Primitive”是一个更广泛、更基础的类别(Class),而“Polygon”只是这个类别下的一个具体类型(Type)。将它们等同,就像说“轿车等同于车辆”一样,虽然轿车是最常见的车辆,但车辆还包括卡车、公交车、摩托车等。
Primitive(基元)是Houdini几何体的基本组成单位之一,它定义了点是如何被连接和解释的。
Houdini支持多种Primitive类型,远不止多边形一种。主要包括:
- Polygon(多边形):由一系列顶点定义的闭合或开放的面。这是最常见的类型。
- Polyline(多边形线):其实是开放的多边形,本质上也是Polygon类型,但通常用来表示曲线。
- Packed Primitives(打包基元):这是一个非常特殊的“指针”或“引用”型基元。它本身只包含极少的信息(如变换信息),但指向了另一份完整的几何体数据(可能在内存中或硬盘上)。这对于处理海量实例或复杂场景至关重要,因为它们内存占用极低。
- Polygon Soup(多边形汤):一种内存优化存储方式,将大量多边形数据紧凑地存放在一起,读取和显示速度快,但编辑性较差。
- Volume(体积)/ VDB:用于表示烟、火、云、雾等体积数据的基元。
- NURBS/Bezier Curves and Surfaces:通过数学公式定义的平滑曲线和曲面。
- Metaballs(融球):可以相互融合的球状场。
- Quadratic Primitives:由数学定义的简单形状,如“原始球体”(Primitive Sphere),它可能只由一个点和半径值定义,非常轻量。
为什么区分这两者至关重要? #
在进行程序化操作和高级开发时,精确区分Primitive的类型是必需的。
程序化判断:在使用VEX或Python时,你经常需要判断一个基元的具体类型,然后执行不同的逻辑。例如,你不能对一个Volume基元执行PolyExtrude操作。通过primintrinsic函数在VEX中可以获取基元的typename,从而判断它是"Poly"、“Volume"还是"Packed"等。
- vex複製
// 在Wrangle节点中判断基元类型
string prim_type = primintrinsic(0, "typename", @primnum);
if (prim_type == "Poly") {
// 执行针对多边形的操作
v@Cd = {1, 0, 0}; // 设为红色
} else if (prim_type == "Volume") {
// 执行针对体积的操作
v@Cd = {0, 0, 1}; // 设为蓝色
}
- 性能优化:理解Packed Primitives和Polygon Soups的特性,是优化复杂场景性能的关键。 [2] 如果你错误地将一个Packed Primitive当作普通Polygon来处理(例如,尝试编辑它的点),将无法得到预期的结果,甚至会破坏其性能优势。
- 工作流程:不同的Primitive类型对应完全不同的工作流程。处理曲线使用
Resample、Carve等节点;处理体积则使用Volume VOP或Volume Wrangle。
